学習内容について
どうも、アロマキャンドルを焚く間がなくて寝不足がちなしがないITエンジニアです。
アロマキャンドル焚くと香りと火の揺らぎでリラックスしてよく眠れるのだが、
零時頃まで作業をしてしまうため焚く間がない。
それでも、焚けば多少寝付きは良くなるのだが寝る時間が減るジレンマ。
今日こそは早く寝たい。

導入はここまでにして問題を見ていこう。
なお、前の問題が見たい方は下記のリンクに移動してほしい。
created by Rinker
¥3,740
(2026/03/01 10:41:00時点 楽天市場調べ-詳細)
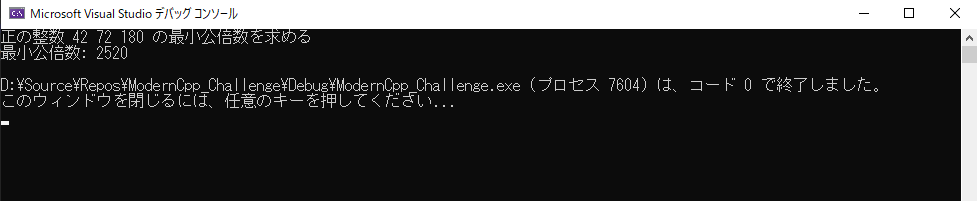
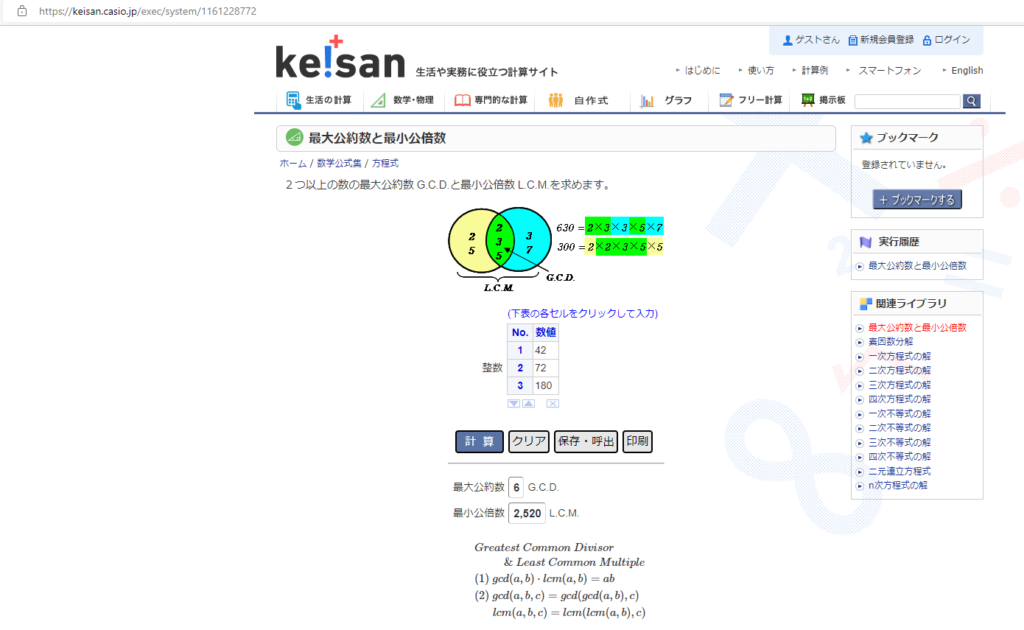
[問題3]最小公倍数
与えられた2個以上の正の整数について、
その最小公倍数を計算して出力するプログラムを書きなさい。
ヒント
解答
解説
最後に
というわけで3問目の問題を学習してみたがいかがだっただろうか。
普段人間がさも当たり前のように求めている最小公倍数ですら、
いざプログラムとして実装しようとすると高度な知識が要求される。
それだけ人間の思考が複雑ということの証左だろう。
いつか人間を超えると散々言われてきたAIがなかなか人間を超えないのもうなづける。
勿論、特化させたAIがその専門分野で人間に勝つのは簡単なのだろうが、
人間本来の強みは思考の柔軟性であって、それこそがAIとの差別化ポイントなのだと思う。
少なくとも現在のAIは人間ほど汎用性があるものは作れていない。
絵を描くために最適化されたAIでは、複雑な文章を理解することは出来ないのである。
まあ、無駄話はここまでにしておこうと思う。
次回はちゃんと解きたいものだ。。。
なお、次の問題については下記リンクに移動してほしい。
第4問目は与えられた正の整数より小さい最大の素数である。


[…] [C++]Modern C++チャレンジの問題を解く~3問目~ […]
[…] [C++]Modern C++チャレンジの問題を解く~3問目~ Modern C++ チャレンジ C++17プログラミング力を鍛える100問 [ Marius Bancila ] created by Rinker ¥3,740 (2022/10/11 11:11:53時点 楽天市場調べ-詳細) […]