学習内容について
どうも、日々眠気と格闘しているしがないITエンジニアです。
本日は、前回に引き続いて
「Modern C++チャレンジ C++17プログラミング力を鍛える100問」の内容を見ていこうと思う。
他の書籍も読み進めてはいるのだが、
Pythonの入門レベルの話をひたすら読み進めているだけなので全くネタに出来ない。。。
導入はここまでにして問題を見ていこう。
前の問題が見たい方は下記のリンクに移動してほしい。
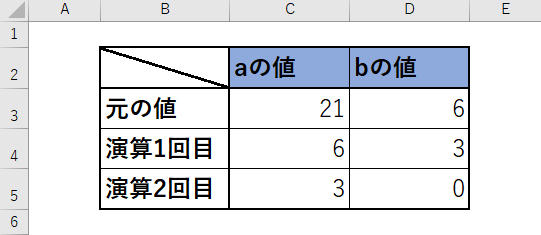
[問題２]最大公約数
与えられた２個の性の整数の最大公約数を計算して出力するプログラムを書きなさい。
ヒント
解答
解説
２つ以上の０でない整数の最大公約数（gcd, greatest common divisor）は、
英語でgreatest common factor（gcf）、highest common factor（hcf）、
greatest common measure（gcm）、highest common divisor（hcd）とも呼びますが、
それらすべての数を割り切ることができる最大の正の整数です。
gcdの計算にはいくつかの方法がありますが、ユークリッドの互除法が効率的です。
実行結果の例では、ａ＝２１、ｂ＝６の最大公約数を求めている。
演算時にａにｂをセットし、ｂにａ÷ｂの余りをセットする。
それをｂが０になるまで繰り返す。そして、演算終了時にａの値が最大公約数である。
１回目の演算結果では、ａ＝６、ｂ＝３になる。
２回目の演算結果では、ａ＝３、ｂ＝０になり、繰り返しが終了しａの値である３が最大公約数となる。
最後に
ちなみに筆者は正しい出力結果にはなるものの、無駄な条件、演算が入っていた。
まだまだ、一流の技術者には程遠いようだ。。。
なお、次の問題については下記リンクに移動してほしい。
第３問目は最小公倍数である。
[…] [C++]Modern C++チャレンジの問題を解く～２問目～ Modern C++ チャレンジ C++17プログラミング力を鍛える100問 [ Marius Bancila ] created by Rinker ¥3,740 (2022/09/17 22:07:01時点 楽天市場調べ-詳細) […]